2022年高考数学试题体现高考改革的要求，突出数学学科特点，强化基础考查，重视数学的本质，服务“双减”政策，助力基础教育提质增效。
试题在各题型起始部分体现面向全体学生，从数学概念、方法入手，注重考查基础知识。但题目的考法更加灵活，如第4题以我国的重大建设成就“南水北调”工程为背景，考查学生的空间想象、运算求解能力，试题引导学生关注社会主义建设的成果，增强社会责任感，体现学生的数学素养。
试题中知识间的结合如函数与数列、切线与不等式、三角变形公式与解三角形的结合体现了良好的区分度，另外难度较高的16、21、22题体现了高考数学的选拔功能，如第22题重视基于数学素养的关键能力的考查，在数学知识层面、数学能力层面和创新思维层面都有所体现。
试题有一定的创新性，平时的立体几何第一问证明，概率统计求概率，解析几何第一问求曲线方程等都有所改变，因此想要在高考中拿到高分，只有深刻挖掘题目背后的原理和内涵，才能更好地把握住数学的本质，在理解数学的基础上学好数学。
2022年高考数学试题，熟悉的“面孔”下有很多不熟悉的“内涵”，单纯靠刷题，靠传统“老题”“老思路”备考是不能很好地应对今年高考题的。基础扎实、思路灵活、运算基本功扎实、真把数学学会的同学能拿高分。

以第7题为例，题目如下：

单纯从题面上来看，就是一个比较大小的问题，平时没少做这类题目，无非是借助0,1等中间量比较，或者借助幂指对函数的单调性，或者作差（商）比较，但入手做，发现不是那回事，三个数都是不超过1的正数。

思路一：观察这几个数的形式，有自然对数，有以e为底的指数式，考虑“切线不等式”，

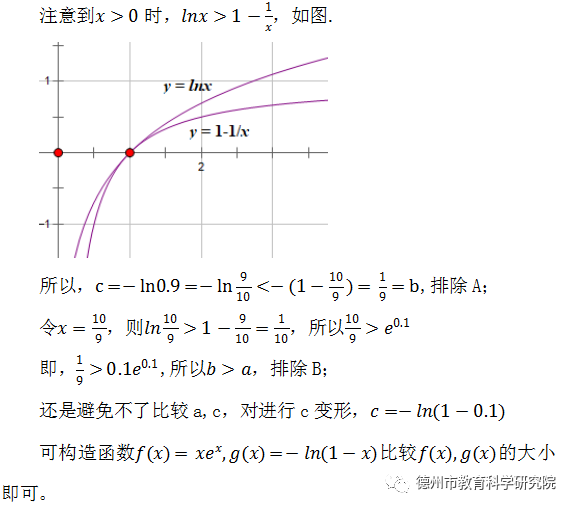
思路二：受上面思路影响，可统一构造函数，如图所示。

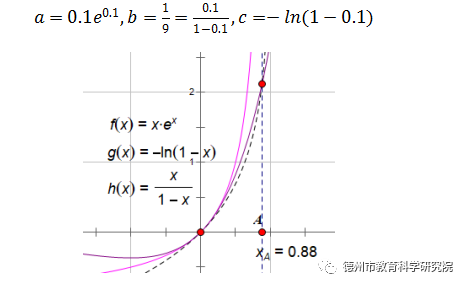
反思：题目找到了思路，分析透了就感觉不难了，但是，关键是找到思路，找到方法。这也就是会题不难。
这个题的解题方法突出了对理性思维的考查，类似的题目，如：

思路三：利用泰勒展开式估值。

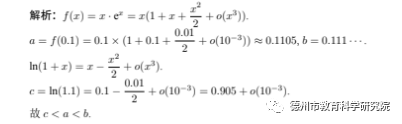
2022年高考数学试题加强对数学核心素养的考查，突出对学科基本概念、基本原理的考查，求新求变反套路，强化对数学本质的考查。在复习备考中加强学生数学思维能力的训练，使学生不仅能够对已知条件变形分析，而且也能对所要求解问题进行变形，再利用已知条件得出正确结论。今年的高考试题突出了对计算能力的考查，数学运算是数学核心素养之一，要加大计算能力的培养，要让学生明白，解数学题“会而不对”与“不会”是同样结果。

德州日报新媒体出品

来源|德州市教育科学研究院 编辑|陈锟 邢仁宇

审核|张燕 终审|李玉梅